Percolación: un cambio de fase geométrico

1 Introducción

La percolación es un fenómeno de la vida cotidiana: el agua en forma de vapor "percola" a través del café molido de la cafetera, se impregna del mismo y nos despierta por la mañana. Si la concentración de café en el filtro fuese extremadamente compacta, el agua no podría percolar pues no encontraría espacios libres entre los poros para hacerlo. En este caso la presión creciente acabaría rompiendo la resistencia del tapón de café por su punto más débil y el agua escaparía por el camino de ruptura así creado, sin impregnarse bien del café. Por este motivo se recomienda no aplastar demasiado el polvo de café con la cucharilla para preparar un buen expresso.

Otros ejemplos de percolación son:

la extracción de petróleo del subsuelo, haciéndolo percolar a través del medio rocoso/poroso bajo el que se encuentra.
la percolación de infecciones o epidemias a través de una población: si la probabilidad de contagio es alta, la infección se "abre paso" o percola en una población dada.

Otro ejemplo, de carácter más físico es el siguiente: imaginemos un retículo de alambre conductor (una alambrada). E imaginemos que se corta un porcentaje de las conexiones entre nudos adyacentes (ver figura 1). Si dicho porcentaje es pequeño y se aplica una diferencia de potencial entre dos lados opuestos de la red, ésta será conductora, y la corriente circulará de un extremo al otro (o del centro a los extremos): la corriente "percola" por la red (ver figura 2 en la que se muestra un camino percolante conectando el centro con el borde). Sin embargo, si el número de enlaces cortados es suficientemente alto, no habrá percolación y el retículo mutilado no podrá conducir de extremo a extremo (o desde el centro a un extremo). Separando estos dos regímenes existe un valor preciso del porcentaje de nodos podados en el que se produce un cambio de fase. De hecho la percolación constituye el cambio de fase más sencillo que uno puede estudiar. Nótese su carácter esencialmente geométrico.

Ejercicio: ¿qué fracción de enlaces hay que quitar de una red unidimensional para que esta deje de ser percolante?

Figure 1: Ejemplos de red de hilo conductor mutilada. En el caso de la izquierda se han eliminado un 30 por ciento de los enlaces y un 70 por ciento en el de la derecha. En el primero hay percolación de enlaces y por tanto conductividad no nula si se aplica una diferencia de potencial entre dos extremos opuestos, mientras que en el de la izquierda el sistema no percola y no hay conducción.

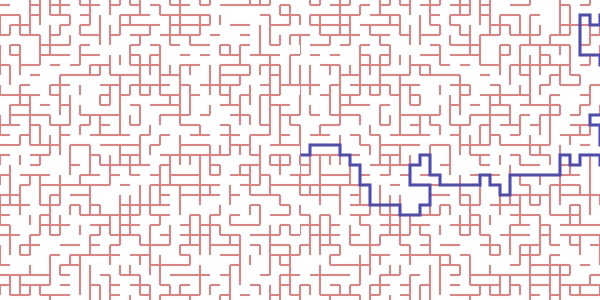
Figure 2: Ilustración de un camino percolatante, conectando el centro de la red con la frontera.

Otras figuras y ejemplos ilustrativos de este fenómeno se pueden encontrar en

http://en.wikipedia.org/wiki/Percolation _ theory

http://ibiblio.org/e−notes/Perc/contents.htm

A un nivel más formal, el concepto de percolación fue introducido por Broadbent en 1954, quien en un simposio sobre métodos Monte Carlo planteó la siguiente pregunta: ¿cuál es la probabilidad de que exista un camino conexo (esto es, un camino "no podado" en el ejemplo anterior) desde un extremo del retículo (o desde el centro) hasta el extremo opuesto? (ver figura 2). Inmediatamente después el problema fue abordado por Hammersley y el mismo Broadbent []. Mientras que en el caso de un retículo unidimensional la solución al problema es trivial, en dos y más dimensiones el problema se hace muy complejo desde el punto de vista analítico, y los estudios numérico/computacionales son esenciales.

Figure 3: Arriba: ejemplos de percolación por nodos en una red hexagonal y percolación por enlaces (izquierda) en una red cuadrada. Se han marcado las distintas agrupaciones o "clusters" conexas (tanto de enlaces como de sitios). Abajo a la izquierda, fase no percolante (las agrupaciones son finitas y no atraviesan todo el sistema). Abajo a la derecha, fase percolante; la agrupación marcada en negro se expande por todo el sistema, esto es, percola.

La importancia de la transición de percolación radica en que está íntimamente relacionada con conceptos fundamentales como fractales e invariancia de escala, y constituye un adecuado banco de pruebas para estudiar técnicas analíticas o numéricas que después serán utilizadas en el estudio de otros cambios de fase más complejos. Por ejemplo, el grupo de renormalización se puede entender partiendo desde modelos percolativos, y os conceptos de tamaño finito, escalado, dimensión fractal, etc., aparecen de manera natural en percolación, como veremos en esta lección.

2 El modelo de percolación más sencillo

Para modelar de forma económica la fenomenología anteriormente descrita se suelen considerar los sencillos modelos de percolación por nodos (o sitios) y percolación por enlaces (véase la figura 3).

Percolación por nodos (o sitios): sea una conjunto de N puntos formando un retículo. Por simplicidad consideraremos normalmente redes cuadradas, pero el modelo es extensible a redes arbitrarias (en la figura 3 arriba a la izquierda, se representa una red hexagonal). Cada nodo ocupado se considera conectado con sus vecinos próximos en la red siempre y cuando éstos estén ocupados también.

Si todos y cada uno de los nodos de la red estén ocupados, se podrá encontrar, obviamente, un camino que conecte cualesquiera dos nodos siguiendo los enlaces. Esta propiedad se mantiene si se elimina al azar una fracción relativamente pequeña de nodos.

Sin embargo, supongamos que en un cierto momento hay una proporción q=1−p (donde p es la probabilidad de que cada nodo esté ocupado) relativamente alta de nodos, con posiciones aleatoriamente distribuidas, que han sido eliminados de la red . Es obvio que si p = 0 o p es muy pequeño, es imposible encontrar un camino que percole a través del sistema.

En este último caso, como se ilustra en la figura 3 (arriba a la izquierda), para un red hexagonal, en la que se representan en distintos colores los distintos caminos conectados, sólo existe caminos limitados, que no atraviesan la red de parte a parte. Los puntos conectados entre sí forman agregados o "clusters".

La parte inferior de la figura 3 ilustra el aspecto de redes no percolantes (izquierda) y percolantes (derecha) para percolación por sitios. Nótese como en el caso no percolante aparecen multitud de agrupaciones de sitios conectados (cada una de un color diferente), mientras que en el caso percolante hay una agrupación (representada en color negro) que se expande por todo el sistema.

De hecho, se puede demostrar analíticamente que, para una red de tamaño infinito, existe un valor crítico de p que llamaremos umbral de percolación, p_c, de forma que si p > p_c existe al menos un camino de nodos interconectados que se extiende por toda la red. Por el contrario, si p < p_c tendremos agrupaciones de nodos interconectados, pero que no se extienden por toda la red.

Un aspecto importante es que p_c, si se determina haciendo experimentos en redes finitas (como es necesariamente el caso en cualquier estudio computacional), depende del tamaño de la red que se considere, puesto que, obviamente, cuanto mayor sea la red, mayor es el valor de p necesario para generar caminos percolantes, que son más largos cuanto mayor sea la red. Dicho de otra manera, un valor p < p_c que genere caminos muy largos pero no infinitos puede parecer que esté en la fase percolante si el tamaño de red que consideramos es pequeño porque los caminos no infinitos abarcan toda la extensión del tamaño considerado y son, por tanto, indistinguibles de caminos percolantes. Esto es lo que se denomina "efectos de tamaño finito"; efectos similares aparecen en las cercanías de todos los puntos críticos. Sin embargo, se puede demostrar que cuando L → ∞, el valor aparente de p_c tiende a un valor bien definido que constituye el punto crítico en tamaño infinito.

Lo que hace interesante a este modelo es comprender lo que ocurre alrededor de p_c y en p_c. En particular, para p = p_c la estructura geométrica del agrupamiento de nodos interconectados más grande tiene estructura fractal. Esta propiedad, así como muchas otras, es debida a que p = p_c es un punto crítico y el sistema tiene un cambio de fase: de fase percolante (o super-crítica) para p > p_c a fase no percolante (o sub-crítica) para p < p_c (ver figura ).

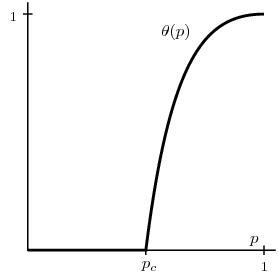
Figure 4: Diagrama que muestra la densidad de sitios en el agregado percolante como función del parámetro de control p: para p < p_c dicha probabilidad es cero (fase no percolante), mientras que para p > p_c la densidad crece monótonamente con p.

Percolación por enlaces: En este caso, todos los sitios están presentes, pero sólo hay enlaces entre ellos con probabilidad p (parte superior derecha de la figura 3; al igual que en el caso anterior, se representan con colores diferentes los distintos caminos conectados; no hay ninguno que atraviese el sistema de parte a parte).

Percolación dinámica: "modelos de incendios forestales"

Los dos modelos introducidos anteriormente (percolación por sitios y percolación por enlaces) son modelos estáticos. Las agrupaciones que generan pueden ser identificadas de una forma "dinámica" utilizando el llamado "modelo de incendios forestales".

Pensemos en un bosque como una red cuadrada en la que cada celda está ocupada por un árbol con probabilidad p, o vacía con probabilidad 1−p. Esta distribución de árboles y huecos será el estado inicial. La caída de un rayo o de una colilla prende fuego en un árbol al azar y, acto seguido, el fuego se extiende propagándose a todos los árboles adyacentes a los que estén ardiendo. Obviamente, cada incendio identifica un agregado del bosque.

Si el fuego puede saltar de un árbol a otro con una cierta probabilidad que depende de la distancia, un problema real muy importante en el diseño de estrategias de preservación forestal y en el de plantaciones de árboles, es el determinar la distancia a la que deben plantarse los árboles para que su densidad sea la mayor posible y, al mismo tiempo, en caso de incendio no arda todo el bosque sino una fracción lo menor posible. La respuesta a esta pregunta (al menos bajo ciertas condiciones) es plantar árboles justo por debajo del umbral de percolación, muy cerca del punto crítico.

Los dos enlaces siguientes muestran visualizaciones del modelo de incendios forestales:

http://demonstrations.wolfram.com/AProbabilisticForestFireModel/

http://upload.wikimedia.org/wikipedia/commons/0/01/Forest_fire_model.gif

2.1 En el punto crítico de percolación emerge un fractal

Justo en el punto crítico se puede demostrar que la agrupación percolante es un fractal. Un fractal es un objeto geométrico cuya "masa", en nuestro caso el número de nodos/árboles) crece al aumentar el tamaño lineal del sistema como una ley de potencias

Figure 5: Agregado percolante en percolación por sitios en una red cuadrada.

M ∼ L^D_f

(1)

donde D_f es la dimensión fractal. Un objeto bidimensional (red cuadrada completamente llena) tendrá dimensión fractal D_f=2, pues al duplicar la longitud el número de nodos se multiplica por 4. Una linea de puntos, tendrá dimensión D_f=1. El agregado mayor de percolación por sitios en el punto crítico, tiene una dimensión fractal

D_f = 1.8958…

(2)

Esto es, se trata de un objeto que interpola entre una línea y una superficie (ver figura 5). Se dice que la "masa" del objeto escala como la longitud elevada a la dimensión fractal. Esto implica que el objeto subyacente es invariante de escala, o lo que es lo mismo auto-similar. La auto-similaridad deriva del hecho de que si cambiamos el tamaño lineal de observación, basta con reescalar la "masa" de un modo adecuado para seguir teniendo la misma ley. Los fractales aparecen en multitud de escenarios en la Naturaleza [].

Información y curiosidades sobre fractales se pueden encontrar en

http://es.wikipedia.org/wiki/Fractal

Figure 6: Fractales en un experimentos de ruptura dieléctrica y de agregación.

La Figura 6 ilustra algunos fractales reales en la Naturaleza. Compárese su aspecto con el del agregado en el umbral de percolación representado en la figura 5.

3 Problemas

Obligatorio: Diseñar y escribir el programa que genere una red cuadrada bidimensional y una los sitios con probabilidad p. Repetir el experimento para distintos tamaños lineales L. Visualizar las configuraciones emergentes (esto es, generar figuras semejantes a las figuras 1, 2 y 3).

Voluntario I: Para distintos tamaños lineales de la red L = 16, L = 32, L = 64 y L = 128 (o más si se desea):

estimar el umbral de percolación p_c(L);
calcular la distribución de probabilidad del número de nodos que pertenecen a un agrupamiento genérico para varios valores de p < p_c, para p = p_c y para varios valores de p > p_c.

Voluntario II: Fijando p = p_c y tomando un tamaño tan grande como sea posible, hallar la dimensión fractal del agregado.

4 Método numérico

4.1 Algoritmo

Lo más directo para generar una configuración el modelo de percolación por sitios donde la proporción 1−p de ellos no funciona sería barrer secuencialmente la red (i,j) donde i y j pueden tomar los valores (1,2,...,L). Con probabilidad p daríamos valor a N(i,j) = 1 y con probabilidad 1−p valor N(i,j) = 0, donde N(i,j) representa que el elemento situado en (i,j) esté funcionando o no respectivamente.

El problema del anterior algoritmo es que generamos una configuración donde conviven agrupamientos grandes y pequeños mezclados entre sí, de forma que para detectar la distribución de tamaños o el agrupamiento más grande hemos de (posteriormente) recurrir a algoritmos sofisticados para su detección. Esto es factible pero complicado.

Aquí vamos a utilizar un método alternativo que genera agrupamientos típicos para un p dado, uno a uno, con lo cual se evita el problema de identificar agregados. Para ello utilizamos un proceso de crecimiento, en el siguiente modo:

Etiquetar todos los puntos de la red como no definidos: N(i,j) = 2; i,j (1,2,...,L). Ocupar un punto del centro del retículo: N(L/2,L/2) = 1.
Generar o modificar la lista de puntos adyacentes (esto es, puntos en contacto directo con el agregado ocupado) y no definidos al agregado. A los adyacentes se les asigna el valor N(i,j)=0. Si la lista no contiene puntos entonces FIN.
Elegir aleatoriamente uno de los puntos del conjunto de adyacentes, (m,n), y considerarlo para el siguiente paso.
Generar un número aleatorio uniforme v [0,1]. Si v < p entonces N(m,n) = 1, Si v > p entonces N(m,n) = 3. Esto es, los puntos de la frontera se añaden al agregado con probabilidad p.
Ir a (2).

De este modo, sólo se definen (encendido o apagado) los nodos de la red correspondientes al agregado central, que se encienden con probabilidad p, como en el modelo original. Iterando el proceso anterior se generan muchas agrupaciones para cada valor dado de p. Es necesario construir un histograma que muestre la distribución de probabilidad de los tamaños de dichos agregados, fijados p y L.

4.2 Estimación del punto crítico

La mejor forma de calcular el punto critico es: estimar (fijados p y L) la fracción, f, de realizaciones (esto es iteraciones del algoritmo anterior) que llegan al borde ¹.

Al representar f frente a p se observará una transición abrupta separando los dos valores límites: f=0 para p pequeño y f=1 para p grande. Se puede identificar el punto crítico p_c(L) con el valor de p para el que f=1/2. Observar que al aumentar el tamaño la transición se hace más y más abrupta. De hecho, es sólo en el límite termodinámico, L → ∞ cuando aparece una singularidad en un punto específico (p_c).

4.3 Estimación de la dimensión fractal del agregado crítico

Para determinar la dimensión fractal, tomar el lado del cuadrado tan grande como sea posible (por ejemplo, L = 512). Generar una configuración usando p=p_c. Contar el tamaño del agregado M(l) solapando con cajas (centradas) de tamaños: l = 10, l = 20, l = 50, l = 100, l = 200. Obviamente al crecer l habrá más y más "masa" del agregado solapando con la caja.

Promediando sobre muchas realizaciones se obtiene una buena estadística. Una vez calculado con precisión el valor medio de M(l) para los distintos valores de l, un simple ajuste de mínimos cuadrados de log(M) frente a log(l) permite determinar la dimensión fractal (para demostrarlo, basta tomar logaritmos en la ecuación (1) y verificar que la ley de potencias se convierte en una línea recta al tomar logaritmos). La pendiente de la recta que mejor se ajuste con los datos en escala doblemente logarítmica debe coincidir con la dimensión fractal.

References

[]: Percolation Structures and Processes, edited by G. Deutsher, R. Zallen y J. Adler, Annals of the Israel Physical Society, Vol. 5 (Hiler, Bristol, 1980).
[]: D. Stauffer y A. Aharony, Introduction to Percolation Theory Taylor and Francis, London (1992); revised 2nd edition (1994).
[]: Geoffrey Grimmett, Percolation, second edition, Springer (1999).
[]: B. Bollobás y Oliver Riordan, Percolation, Cambridge University Press (2006).
[]: Kim Christensen y Nicholas R. Moloney, Complexity and criticality, Imperial College Press (2006).
[]: Harry Kesten, What is ... Percolation?, Notices of the American Mathematical Society, 53 (5), 572-573 (2006).
[]: S. R. Broadbent y J. M. Hammersley, Percolation processe I and II, Proc. Cambridge Philos. Soc. 53, 629 (1957).
[]: B. Mandelbrot, The fractal Geometry of Nature, Freeman, San Francisco (1982).

Footnotes:

¹Para tener suficiente estadística hacer del orden de M = 100 (o más) realizaciones para cada tamaño

File translated from T_EX by T_TH, version 4.03.
On 3 Feb 2014, 12:37.