Resolución de la ecuación de Schrödinger monodimensional

1 Fundamento Teórico

En Mecánica cuántica, el estado físico de un sistema unidimensional de una partícula viene descrito completamente por una función de onda compleja Φ(x,t) que obedece la denominada ecuación de Schrödinger

iħ

∂Φ(x,t)

∂t

⎡
⎣

−

ħ²

∂²

∂x²

+ V(x)

⎤
⎦

Φ(x,t) = HΦ

(1)

donde V(x) es el potencial al que está sometida la partícula, que supondremos que tiene una masa m independiente del tiempo, ħ es la constante de Planck reducida y H es el operador Hamiltoniano, que es hermítico.

La densidad de probabilidad de encontrar a la partícula en un volumen dV alrededor del punto x y en el instante t es

dP=|Φ(x,t)|² dV.

(2)

Para un sistema compuesto únicamente por una partícula, como es el nuestro, la probabilidad total de encontrar la partícula en algún punto del espacio, en cualquier instante t, es igual la unidad,

⌠
⌡

|Φ(x,t)|² dV=1.

(3)

Nótese que la integral de probabilidad es constante durante la evolución temporal, lo que habrá que tenerse en cuenta al plantear la resolución numérica del problema.

Podemos observar que la ecuación de Schrödinger es lineal y que se trata de una ecuación diferencial de primer orden en el tiempo. Para evitar el uso continuado de m y ħ, haremos el cambio de variable t→ tħ en el tiempo y x→ x ħ/√{2m} en el espacio, lo que conduce a una ecuación equivalente a (1) pero en la que ħ = 1 y m=1/2:

−HΦ ≡

⎡
⎣

∂²

∂x²

− V(x)

⎤
⎦

Φ(x,t) = −i

∂Φ

∂t

(4)

Esta ecuación puede resolverse términos de las autofunciones del hamiltoniano H, que, recordemos, es independiente del tiempo. Llamando u_n a los estados acotados y u_k a los estados del continuo, entonces la solución dependiente del tiempo viene dada de forma rigurosa por

Φ(x,t)=

∑
n

a_n e^{−iE_n t} u_n(x) +

⌠
⌡

dk a(k) e^−iE(k)t u_k(x),

(5)

con

a_n=〈u_n,ϕ(x,0)〉, a(k)=〈u_k,ϕ(x,0)〉,

(6)

donde Φ(x,0) es el estado inicial del sistema (y por lo tanto a_n y a(k) son los coeficientes Φ en las bases {u_n} y {u_k}, respectivamente).

De seguir este procedimiento, toparíamos con los inconvenientes de que:

En la mayoría de los casos, las autofunciones y los autovalores del hamiltoniano no se pueden calcular analíticamente y han de determinarse numéricamente.
Por motivos numéricos, el estado inicial debe restringirse necesariamente a una combinación lineal finita de autofunciones y, en cualquier caso, el número de éstas debe ser el menor posible para reducir el trabajo computacional. Truncar la base tiene como inconveniente añadido que la evolución deja de ser unitaria.

Por todo ello, en lugar de seguir el procedimiento anterior integrararemos directamente la ecuación (4). Pero hay que ser muy cuidadosos con el método numérico porque, en general, la discretización provoca que no se conserve la normalización de la función de onda (ecuación 3).

La solución formal de la ecuación de Schroedinger es

Φ(x,t)=e^{−i(t−t₀)H} Φ(x,t₀)

(7)

donde el operador e^−itH es unitario (su inverso coindice con su adjunto) por ser H hermítico. Esta última propiedad será de utilidad a la hora de hallar la discretización más adecuada para resolver el problema numéricamente como veremos a continuación.

2 Problemas

Obligatorio: resolver la ecuación de Schroedinger unidimensional para un potencial cuadrado.
Voluntario: estudiar el coeficiente de transmisión (la probabilidad de encontrar a la partícula al otro lado del obstáculo para tiempos largos pero antes de que se refleje en la pared derecha) en función del parámetro del potencial λ (véase más adelante), para valores positivos y negativos. Estudiar lo mismo para un potencial escalón y uno triangular. Comparar con la teoría.

3 Método numérico

Discretizaremos el espacio y el tiempo tomando x_j=jh y t_n=ns, con j=0,1,...,N y n=0,1,2,...N, donde h es el espaciado en la discretización espacial y s es el espaciado temporal. La función de onda viene dada en cada punto del retículo espacio-temporal por:

Φ(x_j,t_n)→Φ(jh,ns)=Φ_j,n con j=0,1,...,N y n=0,1,2,...,N .

(8)

Supondremos que las condiciones de contorno para la función de onda en j=0 y j=N son las correspondientes a la existencia de un potencial infinito en esos puntos, esto es, la densidad de probabilidad de encontrar la partícula en dichos puntos es cero. Así, Φ_0,n=Φ_N,n=0, en cualquier instante. Puede definirse de forma inmediata un primer algoritmo a partir de la expresión

Φ_j,n+1 = e^{−i s H}Φ_j,n.

(9)

Si s es muy pequeño, el operador de evolución exp(−isH) puede aproximarse por su desarrollo de Taylor a primer orden en t. Si además observamos que el operador Hamiltoniano no es más que la aplicación de una derivada segunda, su discretización espacial es obvia y en total obtenemos el siguiente algoritmo

Φ_j,n+1=(1−isH_D+O(sH_D)²)Φ_j,n,

(10)

donde

Φ_j^′′ ≡

∂² Φ

∂x²

h²

(Φ_j+1−2Φ_j+Φ_j−1)+O(h²)

(11)

y H_D viene dado por

H_D f_j=−

h²

(f_j+1−2f_j+f_j−1)+V_jf_j

(12)

y V_j=V(jh). Este algoritmo tan simple y natural adolece de un grave problema: el operador (1−isH) no es unitario. Esto implica que durante la iteración del algoritmo para encontrar la evolución de la función de onda, la normalización, ∑_j h |Φ_j,n|², irá variando con el tiempo, lo que es incompatible con la restricción de normalización a la unidad expresada en (3) y viola la interpretación de Born. Así pues, el objetivo será encontrar un operador evolución similar al anterior pero que sea unitario. Esto se consigue haciendo uso de la aproximación de Cayley para el operador evolución temporal

e^−isH ≈

1−isH_D/2

1+isH_D/2

(13)

que conduce al algoritmo

Φ_j,n+1=

1−isH_D/2

1+isH_D/2

Φ_j,n.

(14)

Nótese que además de ser unitario, este operador es exacto hasta orden (sH_D)². Para completar el algoritmo, sólo resta diseñar la estrategia para utilizar eficazmente el operador 1/(1+isH_D). Para ello reescribimos la anterior ecuación como

Φ_j,n+1=

⎡
⎣

1+isH_D/2

−1

⎤
⎦

Φ_j,n=χ_j,n−Φ_j,n,

(15)

donde

χ_j,n ≡

1+isH_D/2

Φ_j,n,

(16)

o lo que es lo mismo, dada Φ_j,n, j=0,..,N, χ_j,n es la solución de la ecuación

[ 1+isH_D/2 ]χ_j,n=2Φ_j,n,

(17)

que en forma explícita puede escribirse como

χ_j+1,n+

⎡
⎢
⎣

−2+

−

⎤
⎥
⎦

χ_j,n+χ_j−1,n=

Φ_j,n

(18)

donde ~s=s/h² y ~V_j=h²V_j. De esta forma, el algoritmo de evolución es claro: dada una función de onda en el instante n para toda posición j se resuelve el conjunto de ecuaciones (18) y se obtiene χ_j,n (j=0,..,N). Con esta solución se recurre a la ecuación (15) para obtener las nuevas Φ_j,n+1 (j=0,...,N), iterándose el proceso. Sólo falta por conocer cómo resolver ecuaciones del tipo (18), es decir, cómo invertir matrices tridiagonales.

En este caso, hemos de resolver un conjunto de ecuaciones del tipo

A_j⁻χ_j−1,n+A_j⁰χ_j,n+A_j⁺χ_j+1,n=b_j,n j=1,…,N−1

(19)

donde A_j⁻=1, A_j⁰=−2+2i/~s−~V_j, A_j⁺=1 y b_j,n=4iΦ_j,n/~s. Las condiciones de contorno son χ₀=χ_N=0 (notemos que estas condiciones de contorno implican que en (15) Φ₀ y Φ_N son nulas en cualquier instante).

Para resolver la recurrencia (19) suponemos que su solución es del tipo

χ_j+1,n=α_jχ_j,n+β_j,n j=0,…,N−1

(20)

donde, para garantizar que se cumple χ_N,n=0, tomaremos α_N−1=β_N−1,n=0. Sustituyendo esta expresión en (19) obtenemos

χ_j,n=−

A_j⁻

A_j⁰+A_j⁺α_j

χ_j−1+

b_j,n−A_j⁺β_j,n

A_j⁰+A_j⁺α_j

(21)

Si identificamos las ecuaciones (20) y (21) podemos definir las recurrencias para los coeficientes α y β así

α_j−1=−A_j ⁻γ_j, β_j−1,n=γ_j(b_j,n−A_j⁺β_j,n ).

(22)

donde γ_j⁻¹=A_j⁰+A_j⁺α_j. Estas ecuaciones nos dan la forma de obtener todas las α y β partiendo de j=N−1 y obteniendo en orden decreciente α_j y β_j,n con j=N−2, …,1,0. Obsérvese que α no depende del tiempo y sólo es necesario calcularlas una vez. Una vez obtenidas las α y β, se usa la recurrencia (20) para hallar las χ_j en orden de j crecientes.

Conocida χ_j,n, y con ella Φ_j,n+1, queda discutir qué función de onda inicial se usa y con qué potencial. La función de onda inicial que vamos a usar es una onda plana con una amplitud gaussiana, esto es,

Φ(x,0)=e^ik₀xe^{−(x−x₀)²/2σ²}.

(23)

Notemos que con esta elección, la densidad de probabilidad de encontrar inicialmente la partícula en un punto x es una gaussiana centrada en x₀ y de anchura σ. El número de oscilaciones completas que la función de onda tiene sobre la red depende de k₀, así k₀Nh=2πn_ciclos. En lugar de dar como parámetro inicial k₀, daremos n_ciclos. Obviamente n_ciclos=0,1,....,N. Pero físicamente no tendría mucho sentido que se produjese una oscilación completa de la función de onda entre dos puntos del retículo, pues querría decir que la discretización no es suficientemente fina. Así pues, restringiremos el parámetro n_ciclos a los valores 1,...,N/4. De esta forma, un ciclo tendrá 4 puntos como mínimo. La posición media inicial y la anchura de la gaussiana serán x₀=Nh/4 y σ = Nh/16. Por útimo, el potencial que usaremos tendrá una anchura N/5, estará entrado en N/2 y su altura será proporcional a la energía de la función de onda incidente: λk₀² (puede usarse, por ejemplo, λ = 0.3).

En resumen, utilizando las constantes reescaladas, la función de onda en el retículo se tomará

Φ_j,0=e^{i~k₀ j} e^{−2(4j−N)²/N²},

(24)

donde ~k₀=k₀ h=2πn_ciclos/N donde n_ciclos=1,...,N/4. El potencial es

=V_j h² =

⎧
⎪
⎨
⎪
⎩

si j ∉ [2N/5,3N/5],

2
0

si j ∈ [2N/5,3N/5].

(25)

Sólo queda por fijar el parámetro ~s=s/h². Puesto que la energía es proporcional a k₀² y el operador dinámico discreto tiende a ser exacto en potencias de H s, lo óptimo es elegir ||H||s < 1, esto es, k₀² s < 1. Así deducimos que ~s < 1/~k₀². En particular tomaremos ~s=1/4~k₀². Resumiendo, los parámetro que se han de fijar inicialmente son N, n_ciclos y λ, pues todos los demás se determinan a partir de ellos.

Por lo tanto, el algoritmo para resolver la ecuación de Schrödinger unidimensional puede esquematizarse del siguiente modo:

Dar los parámetros iniciales: N, n_ciclos y λ. Generar ~s, ~k₀, ~V_j, Φ_j,0 (incluyendo las condiciones de contorno Φ_0,0=Φ_N,0=0) y α.
Calcular β utilizando la recurrencia (22).
Calcular χ a partir de (20).
Calcular Φ_j,n+1 de (15).
n=n+1, ir a al paso 2.

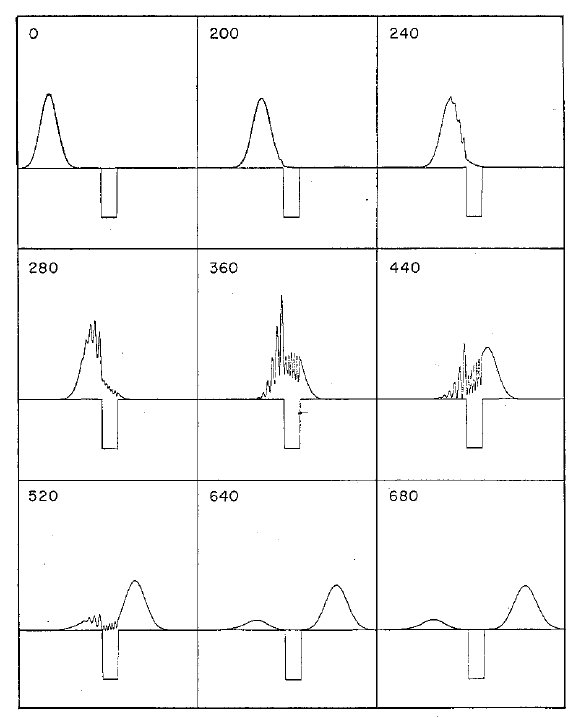
Figure 1: Dispersión de un paquete gaussiano por un pozo cuadrado. La energía media es la mitad de la profundidad del pozo. Los números denotan el tiempo de cada configuración en unidades arbitrarias.

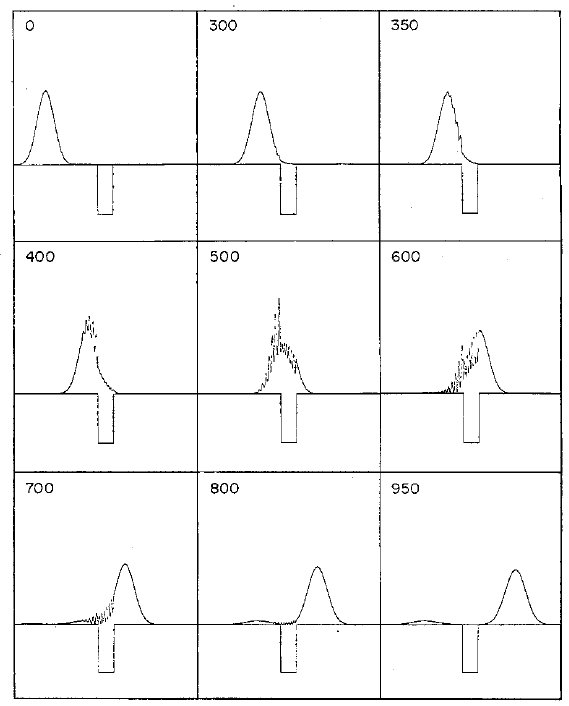
Figure 2: Dispersión de un paquete gaussiano por un pozo cuadrado. La energía promedio es igual a la profundidad del pozo. Los números denotan el tiempo de cada configuración en unidades arbitrarias.

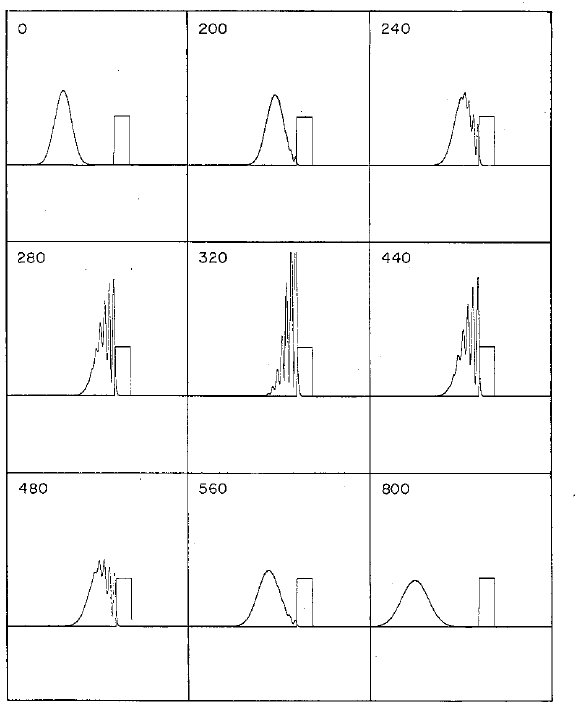
Figure 3: Dispersión de un paquete gaussiano por una barrera cuadrada. La energía promedio es la mitad de la altura de la barrera. Los números denotan el tiempo de cada configuración en unidades arbitrarias.

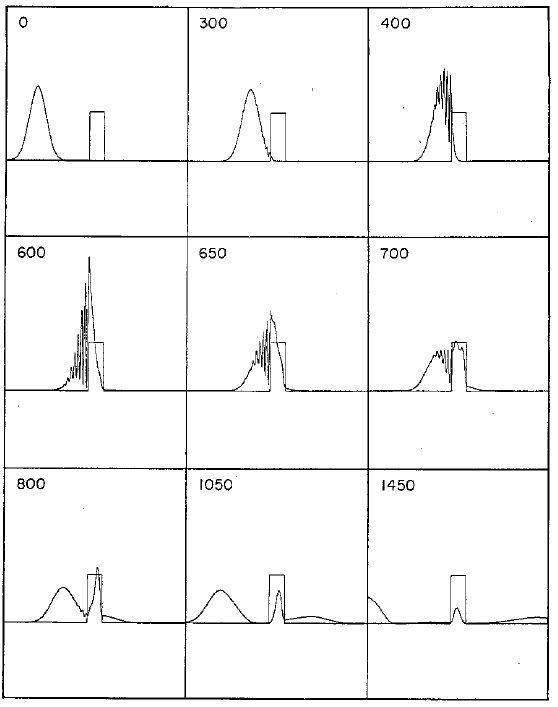
Figure 4: Dispersión de un paquete gaussiano por una barrera cuadrada. La energía promedio es igual a la altura de la barrera. Los números denotan el tiempo de cada configuración en unidades arbitrarias.

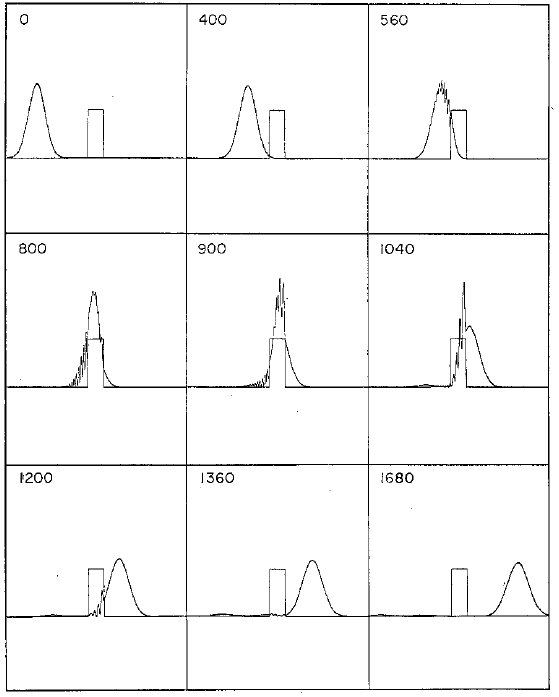
Figure 5: Dispersión de un paquete gaussiano por un pozo cuadrado. La energía promedio es dos veces la altura de la barrera. Los números denotan el tiempo de cada configuración en unidades arbitrarias.

Números complejos en Fortran.

Declaración: implicit double complex (h)
Asignación de valores constantes: h=(1.0d+0,0.3d+0) (=1+i0.3).
Asignación de variables: h=complex(a,b) (=a+ib).

File translated from T_EX by T_TH, version 4.03.
On 3 Feb 2014, 13:21.